Contents
1. 전통적인 링크 예측
1.1 휴리스틱 방법론
1.2 Matrix factorization
2. GNN 기반 링크 예측
2.1 GAE (Graph Autoencoder)
2.2 VGAE (Variational Graph Autoencoder)
링크 예측(Link Prediction)은 그래프 이론의 중요한 분야 중 하나입니다. 링크 예측은 그래프 내에서 새로운 연결이 형성될 가능성을 예측하는 작업으로, 소셜 네트워크와 추천 시스템에 핵심적으로 사용되고 있습니다. 특히 추천 시스템에서 유저 노드와 아이템 노드 간의 상호작용을 예측하기 위해 활용됩니다. 이번 포스팅에서는 그래프 구조에서 링크 예측을 위한 기초적인 방법론부터 GAE 신경망까지 알아보도록 하겠습니다. 기초적인 방법론은 딥러닝 학습 없이, 수학적 모델로 링크 예측을 수행합니다. 이후 행렬 분해를 통한 방법론을 알아보고, 마지막으로 GNN을 기반으로 한 GAE (Graph Autoencoder)와 VGAE (Variational Graph Autoencoder)를 소개하고 VGAE를 코드로 구현하겠습니다.
1. 전통적인 링크 예측
링크 예측 문제는 예전부터 그래프 관련 연구의 관심사였습니다. 먼저 GNN 기반 모델을 살펴보기 전에 전통적인 링크 예측 방법론을 소개하겠습니다. 먼저, 로컬 및 글로벌 이웃에 기반한 휴리스틱 방법론을 살펴보겠습니다. 다음으로 행렬 분해와 DeepWalk, Node2Vec 관련 링크 예측을 알아보겠습니다.
1.1 휴리스틱 방법론
휴리스틱 기법은 노드 간의 링크를 예측하기 위한 간단하고 실용적인 방법입니다. 수학적 이해를 통해 직관적으로 이해하기 쉬운 방법론입니다. 휴리스틱 기법은 이웃이 떨어진 정도를 의미하는 홉(hop)의 수에 따라 분류할 수 있습니다. 나이브한 기법은 노드에 인접한 1-hop 이웃만을 필요로 하며, 더 복잡한 기법은 2-hop 이웃이나 전체 그래프도 고려합니다. 여기서는 로컬(1-hop)과 글로벌 휴리스틱으로 나누어 설명하겠습니다.

로컬 휴리스틱(local heuristics)은 해당 노드의 로컬 이웃을 고려하여 두 노드 간의 유사성을 측정합니다.
- Common neighbors: 공통 이웃은 가장 단순히 두 개의 노드가 공통으로 가지는 이웃의 수(1-hop)를 세는 것입니다. 이 방법에 따르면, 공통 이웃이 많을수록 두 노드가 연결될 가능성이 더 높습니다.
$$ f(u,v) = \left| N(u)\cap N(v) \right| $$
- Jaccard’s coefficient: 자카드 계수는 두 개의 노드가 공유하는 이웃의 비율(1-hop)을 측정합니다. 이는 위의 공통 이웃과 같은 아이디어를 기반으로 하지만, 결과를 이웃의 총 수로 정규화된 다는 것이 차이점 입니다. 이는 높은 차수의 노드보다는 연결된 이웃이 적은 노드를 잘 평가하는 장점이 있습니다.
$$ f(u,v) = \frac{\left| N(u)\cap N(v)\right|}{\left| N(u)\cup N(v)\right|} $$
- Adamic–Adar index: 아다믹-아다르 지수는 두 개의 대상 노드가 공유하는 이웃의 역 로그 차수를 합산합니다(2-hop). 이 방법은 큰 이웃을 가진 공통 이웃은 작은 이웃을 가진 공통 이웃보다 덜 중요하다는 것을 반영합니다. 이는 단순히 이웃이 많은 노드여서 공통 노드로 묶으는 것을 완화합니다.
$$ f(u,v) = \sum_{x \in N(u) \cap N(v)} \frac{1}{log\left| N(x) \right|} $$
위에서 알아본 로컬 휴리스틱 기법은 이웃 노드의 차수에 의존하는 방법론입니다. 이는 연산 속도와 설명력에는 정점이 있지만, 더욱 복잡한 관계를 포착하기에는 제한됩니다.
이러한 한계를 해결하기 위해, 글로벌 휴리스틱(global heuristic) 방법론은 로컬 이웃이 아닌 전체 네트워크를 고려합니다.
- Katz index: 카츠 인덱스는 두 노드 사이의 모든 가능한 경로의 가중 합을 계산합니다. 가중치는 감소 인자인 베타(β ∈ [0,1]로 표현하며, 더 멀리 떨어진 경로에 벌점을 주기 위해 사용됩니다. 이 정의에 따라 두 노드는 많은(비교적 짧은) 경로가 있을수록 연결될 가능성이 더 높습니다. 어떤 길이의 경로든 인접 행렬의 거듭제곱( \(A^n\) )을 사용하여 계산할 수 있기 때문에 카츠 지수는 다음과 같이 정의됩니다.
$$ f(u,v) = \sum_{i=1}^{\infty} \beta^i A^i $$
Note
길이가 2인 경로는 인접 행렬의 제곱(\(A^2\))으로, 길이가 3인 경로는 인접 행렬의 세제곱(\(A^3\))으로 나타낼 수 있습니다. 경로가 더 길어져도 마찬가지로 표현할 수 있습니다.
- Random walk with restart: Random Walk with Restart (RWR)는 대상 노드에서 시작하여 랜덤하게 이웃 노드를 탐색하는 과정을 반복합니다. 각 노드를 방문할 때마다 방문 횟수를 증가시키고, 일정 확률(α)로 워크를 대상 노드에서 다시 시작합니다. 일정 확률로 대상 노드에서 워크를 다시 시작하기 때문에, 대상 노드와 관련이 높은 노드에 집중할 수 있습니다. RWR은 미리 정의된 반복 횟수 또는 정지 조건까지 진행한 후, 대상 노드와 방문 횟수가 가장 높은 노드들 간에 링크를 예측합니다. 방문 횟수가 높은 노드들은 대상 노드와의 관련성이 높을 가능성이 있기 때문에, 이를 통해 링크 예측을 수행할 수 있습니다.
1.2 Matrix factorization
링크 예측을 위한 행렬 분해는 넷플릭스의 추천시스템 연구에서 영감을 받아 등장했습니다. 추천시스템에서 사용자-아이템 평점 행렬을 분해하는 것과 유사하게, 전체 인접 행렬 \(\tilde A\) 를 예측함으로써 링크를 간접적으로 예측합니다. 이를 위해 노드 임베딩을 사용합니다. 비슷한 노드와는 비슷한 임베딩을 가져야 하므로, 노드와는 각각 유사한 임베딩을 가져야 합니다. 이를 내적을 사용하여 다음과 같이 표현할 수 있습니다.
- 만약 노드들이 유사하다면, 잠재 벡터의 곱인 \(z_v^T z_u\)은 최대화 되어야 합니다.
- 만약 노드들이 다르다면, 잠재 벡터의 곱인 \(z_v^T z_u\)은 최소화 되어야 합니다.

이러한 방법론을 matrix factorization 이라고 하며, 인접 행렬 을 두 개의 행렬의 곱으로 분해합니다. 목표는 그래프 G = (V,E)의 실제 요소 값들과 예측된 요소 간의 L2 노름을 최소화하는 노드 임베딩을 학습하는 것입니다.
$$ minimize \sum_{i \in V, j \in V} (A_{uv} - z_v^T z_u)^2 $$
2. GNN 기반 링크 예측
위에서는 전통적인 링크 예측 방법론들을 살펴보았습니다. 이번에는 neural network를 기반으로 링크 예측을 위한 두 가지 GNN 아키텍처를 소개하겠습니다. 이미지 분야에서 유명한 오토인코더(Autoencoder) 기법을 활용한 모델인, 그래프 오토인코더 (GAE)와 변분 그래프 오토인코더 (VGAE)를 살펴보겠습니다.
2.1 GAE (Graph Autoencoder)
GAE는 인코더(encoder) - 디코더(decoder) 두 가지 모듈로 구성 됩니다.
특히 오토인코더는 인풋과 아웃풋이 같은 것이 특징입니다. 이러한 인코더, 디코더 학습을 통해 이미지나 그래프 데이터에 대한 잠재 특성을 얻는 것이 오토인코더 모델의 목적입니다.
GAE에서는 그래프 데이터를 잠재 공간으로 투영하는 과정을 거칩니다. 인코더는 그래프 데이터의 특성을 추출하고 잠재 공간으로 투영하는 역할을 수행하며, 디코더는 잠재 공간의 표현을 사용하여 링크 예측을 수행합니다. 이러한 구조를 통해 GAE 신경망은 그래프의 구조와 특성을 동시에 고려하여 링크 예측을 수행할 수 있습니다.
- 인코더(encoder)는 노드 임베딩을 학습하기 위한 기본적인 GCN 레이어로 이루어 집니다.
- 디코더(decoder)는 위에 알아본, matrix factorizaion 기법을 통해 인접 행렬(adjacency matrix)를 근사합니다. 이때 최종 아웃풋에는 시그모이드(sigmoid) 함수(\(\))를 적용합니다.
오토인코더의 목적은 노드나 그래프를 분류하는 것이 아닌 것을 리마인드 해야 합니다. 오토인코더는 인접 행렬 \(\tilde A\)의 각 요소에 대한 확률 [0,1]을 예측하는 것입니다. 따라서 마지막 활성화 함수에는 시그모이드를 적용하고, 손실 함수로 binary cross-entropy loss를 사용합니다.
하지만 인접 행렬은 종종 매우 희소하기 때문에 GAE는 대부분 0값을 예측하는 편향을 가지게 됩니다. 이러한 편향을 해결하기 위해 두 가지 간단한 기법이 있습니다. 첫째, 이전의 손실 함수에서 = 1을 선호하는 가중치를 추가할 수 있습니다. 둘째, 훈련 중에 0 값을 적게 샘플링하여 레이블을 더 균형있게 만들 수 있습니다.
또 다른 가능한 개선 방법으로는 GAE를 확률적인 변형인 변분 GAE (Variational GAE)로 변환하는 방법을 알아보겠습니다.
2.2 VGAE (Variational Graph Autoencoder)
이미지에서도 오토인코더(AE)와 변분 오토인코더(VAE)의 차이를 완전히 이해하는 것이 쉽지 않습니다. 이해를 위해 조금 단순히 정리하자면, VAE는 데이터의 분포, 즉 확률을 학습하는 것으로 간단히 표현할 수 있습니다. 그래프에서는, GAE가 그래프의 구조적 정보를 반영하기 위해 노드 임베딩을 직접 학습하는 것을 목표로 한다면, VGAE는 학습된 임베딩의 불확실성을 포착하기 위해 정규 분포를 학습합니다.
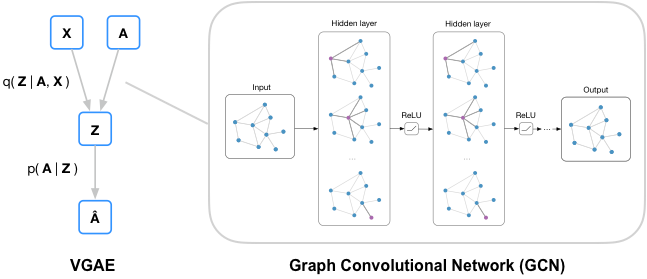
기본적으로 AE(autoencoder) 기반 모델들은 조건부 확률을 기반으로 합니다. VAGE에서 사용하는 손실 함수는 아래에서 설명드리겠습니다. VGAE는 변분 추론(variational inference)을 기반으로 합니다. 변분 추론은 확률 분포의 추정을 위해 가우시안 분포와 같은 확률 분포의 파라미터를 학습하는 방법입니다. VGAE는 그래프의 인접 행렬과 특성 행렬을 입력으로 사용하고, 그래프의 잠재 변수를 추정하기 위해 인코더 네트워크를 통해 그래프 데이터를 잠재 벡터로 투영합니다.
VGAE의 핵심은 잠재 변수의 확률적 표현입니다. 잠재 변수를 평균과 분산으로 모델링하여 노드 임베딩의 불확실성을 포착 하는 것입니다. 이러한 학습을 통해, 새로운 링크를 예측한다는 것이 목표라는 것을 다시 리마인드 하면 좋겠습니다. VGAE 역시 인코더와 디코더, 두 개의 모듈로 구성됩니다.
- 인코더(encoder)는 첫 번째 레이어를 공유하는 두 개의 GCN 레이어로 구상됩니다. 구체적으로 인코더의 목표는 각 잠재 정규 분포의 매개 변수인 평균 μ과 분산 \(\sigma ^2\)을 학습하는 것입니다.
- 디코더(decoder)는 학습된 분포 (μ, sigma^2)를 사용하여 임베딩을 샘플링하고, 잠재 변수 간의 동일한 내적을 사용하여 인접 행렬을 근사화합니다. 디코더는 잠재 변수 간의 내적을 사용하여 근사적으로 인접 행렬을 계산합니다.
VGAE는 학습하는 파라미터가 평균과 분산이기 때문에, 손실 함수도 이에 맞추어 적용해야 합니다. 이를 위해 Kullback-Leibler (KL) divergence를 사용합니다. KL divergence는 두 분포의 차이를 측정합니다. 이를 ELBO, Evidence Lower Bound라고 표현할 수도 있습니다.
$$ L_{ELBO} = L_{BCE} - KL[q(Z| X,A) \| p(Z)] $$
그렇다면 VGAE 아키텍처를 코드로 구현해보겠습니다.
- T.NormalizeFeatures: 인풋 데이터 x의 features를 정규화합니다
- 데이터 세트에서 엣지 데이터를 랜덤하게 스플릿합니다. (85/5/10)
- add_negative train_samples: 데이터셋이 이미 negative sampling 돼있기 때문에 False.
import torch
!pip install -q torch-scatter~=2.1.0 torch-sparse~=0.6.16 torch-cluster~=1.6.0 torch-spline-conv~=1.2.1 torch-geometric==2.2.0 -f https://data.pyg.org/whl/torch-{torch.__version__}.html
torch.manual_seed(0)
torch.cuda.manual_seed(0)
torch.cuda.manual_seed_all(0)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
import numpy as np
np.random.seed(0)
import torch
torch.manual_seed(0)
import matplotlib.pyplot as plt
import torch_geometric.transforms as T
from torch_geometric.datasets import Planetoid
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
transform = T.Compose([
T.NormalizeFeatures(),
T.ToDevice(device),
T.RandomLinkSplit(num_val=0.05, num_test=0.1, is_undirected=True, split_labels=True, add_negative_train_samples=False),
])
dataset = Planetoid('.', name='Cora', transform=transform)
train_data, val_data, test_data = dataset[0]
세 가지 GCN 레이어를 사용합니다.
- a shared layer
- a sencond layer (to approximate mean values)
- a third layer (to approximate variance value - log_std)
from torch_geometric.nn import GCNConv, VGAE
class Encoder(torch.nn.Module):
def __init__(self, dim_in, dim_out):
super().__init__()
self.conv1 = GCNConv(dim_in, 2 * dim_out)
self.conv_mu = GCNConv(2 * dim_out, dim_out)
self.conv_logstd = GCNConv(2 * dim_out, dim_out)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index).relu()
return self.conv_mu(x, edge_index), self.conv_logstd(x, edge_index)
- 이후에 VGAE에 encoder를 인풋으로 사용합니다.
- decoder는 default로 inner product를 적용합니다.
model = VGAE(Encoder(dataset.num_features, 16)).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
- train() function은 model.encode()를 통해 임베딩 매트릭스 Z를 생성합니다.
- 이후 ELBO loss를 계산하기 위해 model.recon_loos를 사용합니다.
- 또한 kl_loss, KL divergence를 계산합니다.
model = VGAE(Encoder(dataset.num_features, 16)).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
def train():
model.train()
optimizer.zero_grad()
z = model.encode(train_data.x, train_data.edge_index)
loss = model.recon_loss(z, train_data.pos_edge_label_index) + (1 / train_data.num_nodes) * model.kl_loss()
loss.backward()
optimizer.step()
return float(loss)
@torch.no_grad()
def test(data):
model.eval()
z = model.encode(data.x, data.edge_index)
return model.test(z, data.pos_edge_label_index, data.neg_edge_label_index)
for epoch in range(301):
loss = train()
val_auc, val_ap = test(test_data)
if epoch % 50 == 0:
print(f'Epoch {epoch:>2} | Loss: {loss:.4f} | Val AUC: {val_auc:.4f} | Val AP: {val_ap:.4f}')
test_auc, test_ap = test(test_data)
print(f'Test AUC: {test_auc:.4f} | Test AP {test_ap:.4f}')
### result ###
Epoch 0 | Loss: 3.4890 | Val AUC: 0.6745 | Val AP: 0.7105
Epoch 50 | Loss: 1.3233 | Val AUC: 0.6723 | Val AP: 0.7042
Epoch 100 | Loss: 1.1533 | Val AUC: 0.7363 | Val AP: 0.7445
Epoch 150 | Loss: 1.0835 | Val AUC: 0.7774 | Val AP: 0.7771
Epoch 200 | Loss: 1.0081 | Val AUC: 0.8343 | Val AP: 0.8278
Epoch 250 | Loss: 0.9793 | Val AUC: 0.8501 | Val AP: 0.8502
Epoch 300 | Loss: 0.9511 | Val AUC: 0.8611 | Val AP: 0.8589
Test AUC: 0.8611 | Test AP 0.8589
- 마지막으로 인접 행렬 \(\tilde{A}\)를 구합니다.
z = model.encode(test_data.x, test_data.edge_index)
Ahat = torch.sigmoid(z @ z.T)
Ahat
### result ###
tensor([[0.7858, 0.6646, 0.7677, ..., 0.6396, 0.8112, 0.8074],
[0.6646, 0.8023, 0.8126, ..., 0.4137, 0.7391, 0.6960],
[0.7677, 0.8126, 0.8576, ..., 0.5275, 0.8361, 0.8076],
...,
[0.6396, 0.4137, 0.5275, ..., 0.7742, 0.6965, 0.7088],
[0.8112, 0.7391, 0.8361, ..., 0.6965, 0.8744, 0.8612],
[0.8074, 0.6960, 0.8076, ..., 0.7088, 0.8612, 0.8529]],
grad_fn=<SigmoidBackward0>)
링크 예측(link prediction)은 그래프 이론의 중요한 분야입니다. 본 포스팅에서는 기본적인 링크 예측 방법론과 GNN 기반 방법론을 알아보았습니다. 또한 VGAE 아키텍처를 코드로 구현하여 그래프 내의 새로운 연결을 예측하는 방법을 알아보았습니다. VGAE는 그래프의 구조와 특성을 고려한 잠재적 표현을 학습하여 링크 예측 성능을 향상시킵니다. 이를 통해 소셜 네트워크, 추천 시스템 등 다양한 분야에 활용 될 수 있습니다. 이상으로 포스팅 마치겠습니다. 감사합니다.
Reference
Hands-On Graph Neural Networks Using Python, published by Packt.
Kipf, T. N., & Welling, M. (2016). Variational graph auto-encoders. arXiv preprint arXiv:1611.07308.
'Graph > Graph with Code' 카테고리의 다른 글
| 11. Heterogeneous Graphs 코드로 구현하기 (2) | 2023.07.11 |
|---|---|
| 10. GNN을 활용한 그래프 생성 코드 구현하기 (0) | 2023.07.10 |
| 8. GIN (Graph isomorphism network) 기초 및 코드 구현 (0) | 2023.07.03 |
| 7. GraphSAGE 이해 및 코드 구현 (7) | 2023.06.30 |
| 6. Graph Attention Networks (GATs) 기초 및 코드 구현 (0) | 2023.06.29 |

