Contents
1. GIN (Graph Isomorphism Network)
2. GIN을 활용한 그래프 분류
2.1 코드 구현
GIN은 Graph Isomorphism Network의 약자로, 그래프 동형성을 바탕으로한 모델입니다. 2018년에 Xu et al.에 의해 소개된 GIN은 그래프 동형성을 평가하는 WL 테스트의 표현을 갖추도록 설계되었습니다. 본 포스팅에서는 WL 테스트에 대한 설명은 다루지 않습니다. 전통적인 방식보다는, neural network 관점에 포커싱하여 GIN을 소개합니다. GIN은 그래프 구조를 구별하기 위해 사용되는 기법입니다. 이번 포스팅에서는 GIN과 그래프의 표현력을 의미하는 graph expressiveness에 대해 설명하겠습니다.
1. GIN (Graph Isomorphism Network)
그래프 표현력(Graph Expressiveness)은 그래프 신경망(GNN)에서 알아야 할 중요한 개념중 하나입니다. 그래프 표현력은 GNN이 그래프의 특징과 구조를 효과적으로 표현하고 모델링할 수 있는 능력을 의미합니다. GNN에서의 표현력은 인접 노드 정보를 aggregation하는 함수에 따라 달라집니다.
GIN이 소개된 “How Powerful are Graph Neural Networks? (Xu et al. 2018)” 논문에서는 aggregation을 다음과 같은 두 가지 함수로 일반화 합니다.
Xu, K., Hu, W., Leskovec, J., & Jegelka, S. (2018). How powerful are graph neural networks?. arXiv preprint arXiv:1810.00826.
- Aggregate: Aggregation 함수는 GNN 아키텍처에서 고려할 이웃 노드를 선택합니다.
- Combine: 수식에서 ϕ로 나타내는 combine 함수는 선택된 노드들의 임베딩을 결합하여 타겟 노드의 새로운 임베딩을 생성합니다.
두 함수에 따라 노드 \(i\)의 임베딩은 아래 식과 같이 표현할 수 있습니다.
$$ \acute{h_i} = \phi (h_i, f(\{{h_j}:j \in N_i\}))$$
GCN의 경우에 \(f\) 함수는 모든 이웃을 aggregate하고, \(\phi\)는 mean 함수입니다. GraphSAGE의 경우에는 \(f\)가 이웃 샘플링 함수가 되고, \(\phi\)는 mean, LSTM, max 함수가 됩니다. 이전 포스팅들을 참고하시면, 이 부분이 잘 이해되실 것이라고 생각합니다.
GIN에서는 이 두 함수가 모두 일대일 대응되어야 한다고 말합니다. 일대일 대응 함수는 서로 다른 입력을, 서로 다른 출력으로 매핑합니다. 그래프를 구별하기 위해서는, 그래프의 특성을 이런 식으로 서로 다른 출력값으로 나타내어야 합니다. 만약 이 두 함수가 일대일 대응이 아니라면, 서로 다른 입력에 대해 같은 출력을 얻게 됩니다. 이 경우에는 임베딩이 가지는 표현력이 줄어들 것입니다.

GIN에서는 이 두 함수를 설계하기 위해 값을 approximate 하는 방법을 적용합니다.
Universial approximation theorem에 의해, MLP 구조를 통해 두 함수를 모두 학습할 수 있습니다.
NOTE
Universial approximation theorem에 따르면, 하나의 은닉층(hidden layer)을 가진 피드포워드 신경망은 충분한 수의 뉴런(neuron)과 적절한 가중치(weight)를 가질 경우, 어떤 연속적인 함수든지 원하는 정확도로 근사화할 수 있습니다. 즉, 신경망은 주어진 입력과 출력 사이의 복잡한 비선형 관계를 학습하고 모델링할 수 있다는 것을 의미합니다. 이 정리는 1980년대에 George Cybenko와 Kurt Hornik에 의해 독립적으로 증명되었으며, 신경망의 히든 레이어의 뉴런 수가 충분하면 임의의 연속 함수를 원하는 정확도로 근사화할 수 있음을 보여줍니다. 이후에는 더 일반적인 다층 퍼셉트론(multilayer perceptron)이나 딥러닝 신경망의 경우에도 유사한 근사화 성질이 있다는 것이 알려져 있습니다.
Universial approximation theorem에 의해 GIN에서의 aggregate와 combine 함수는 아래와 같은 MLP 레이어로 나타낼 수 있습니다.
$$\acute{h_i} = MLP((1+\epsilon) \bullet h_i + \sum_{j\in{N_i}}h_j)$$
이 식에서 엡실론은 이웃 노드와 비교하여, 타겟 노드의 중요도를 나타내는 학습 파라미터입니다.
2. GIN을 활용한 그래프 분류
이번에는 GIN을 활용하여 노드 임베딩에 global pooling 기법을 적용하고, 그래프 임베딩으로 나타내는 방법을 소개합니다. 이후 GIN 기법을 PROTEINS 데이터셋에 적용해보겠습니다. 그래프 분류를 위해, 노드 임베딩을 global pooling 기법을 사용하여 하나의 그래프 임베딩으로 나타냅니다.
각 노드의 임베딩 값들을 사용하여 그래프를 임베딩 하는 것을 global pooling 또는 graph-level readout 이라고 합니다.
그래프 분류 작업은 GNN을 통해 생성된 노드 임베딩을 기반으로 합니다. 다음과 같은 세가지 방법으로 그래프 임베딩을 타나냅니다.
- Mean global pooling: 그래프 임베딩 \(h_G\)을 모든 노드 임베딩의 평균으로 나타냅니다.
$$h_G = \frac{1}{N} \sum_{i=0}^{N}h_i$$
- Max global pooling: 각 노드 dimension에서 가장 높은 같을 그래프 임베딩으로 나타냅니다.
$$h_G = max_{i=0}^N(h_i)$$
- Sum global pooling: 모든 노드의 합으로 그래프 임베딩을 나타냅니다.
$$h_G = \sum_{i=0}^{N}h_i$$
Mean 풀링과 max 풀링은 임베딩에 대해 한정적인 정보만 가져오기 때문에 graph expressiveness가 줄어듭니다. 일반적으로 sum global pooling이 표현력이 좋지만, GIN에서는 모든 노드 임베딩의 구조적인 정보를 활용하기 위해 모든 레이어 단계마다의 풀링 정보를 concatenate한 sum global pooling을 적용합니다.
$$h_G = \sum_{i=0}^{N}h_i^0 \left| \right| \cdots \left| \right| \sum_{i=0}^{N}h_i^k $$
이러한 수식을 통해 각 레이어의 memory를 결합하는 방식으로 그래프의 전역정인 특징을 캡처하면서, 동시에 각 노드의 정보를 유지합니다.
2.1 코드 구현
앞서 소개한 grapg-level readout 함수와 GIN 모델을 PROTEINS [5,6,7] 데이터셋에 적용해보겠습니다.
데이터셋은 프로틴 구조를 나타내는 1,113개의 그래프와, 아미노산을 나타내는 각 노드로 구성됩니다.
두 아미노산, 노드의 거리가 0.6 나노미터보다 작으면 엣지로 연결되며, 이 데이터셋의 목표는 각 프로틴을 enzyme로 분류하는 것입니다.
먼저 필요한 라이브러리와 데이터셋을 불러옵니다.
import torch
!pip install -q torch-scatter~=2.1.0 torch-sparse~=0.6.16 torch-cluster~=1.6.0 torch-spline-conv~=1.2.1 torch-geometric==2.2.0 -f https://data.pyg.org/whl/torch-{torch.__version__}.html
torch.manual_seed(11)
torch.cuda.manual_seed(0)
torch.cuda.manual_seed_all(0)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
from torch_geometric.datasets import TUDataset
dataset = TUDataset(root='.', name='PROTEINS').shuffle()
# Print information about the dataset
print(f'Dataset: {dataset}')
print('-----------------------')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of nodes: {dataset[0].x.shape[0]}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')
### result ###
Dataset: PROTEINS(1113)
-----------------------
Number of graphs: 1113
Number of nodes: 139
Number of features: 3
Number of classes: 2
이후 데이터를 80/10/10 비율로 분할합니다.
from torch_geometric.loader import DataLoader
# Create training, validation, and test sets
train_dataset = dataset[:int(len(dataset)*0.8)]
val_dataset = dataset[int(len(dataset)*0.8):int(len(dataset)*0.9)]
test_dataset = dataset[int(len(dataset)*0.9):]
print(f'Training set = {len(train_dataset)} graphs')
print(f'Validation set = {len(val_dataset)} graphs')
print(f'Test set = {len(test_dataset)} graphs')
# Create mini-batches
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=True)
print('\nTrain loader:')
for i, batch in enumerate(train_loader):
print(f' - Batch {i}: {batch}')
print('\nValidation loader:')
for i, batch in enumerate(val_loader):
print(f' - Batch {i}: {batch}')
print('\nTest loader:')
for i, batch in enumerate(test_loader):
print(f' - Batch {i}: {batch}')
### result ###
Training set = 890 graphs
Validation set = 111 graphs
Test set = 112 graphs
Train loader:
- Batch 0: DataBatch(edge_index=[2, 8388], x=[2227, 3], y=[64], batch=[2227], ptr=[65])
...
- Batch 13: DataBatch(edge_index=[2, 9736], x=[2644, 3], y=[58], batch=[2644], ptr=[59])
Validation loader:
- Batch 0: DataBatch(edge_index=[2, 8118], x=[2221, 3], y=[64], batch=[2221], ptr=[65])
- Batch 1: DataBatch(edge_index=[2, 4892], x=[1330, 3], y=[47], batch=[1330], ptr=[48])
Test loader:
- Batch 0: DataBatch(edge_index=[2, 7868], x=[2097, 3], y=[64], batch=[2097], ptr=[65])
- Batch 1: DataBatch(edge_index=[2, 8920], x=[2376, 3], y=[48], batch=[2376], ptr=[49])
GIN 모델에는 최소 2개의 MLP 레이어가 필요합니다.
논문에 따라 각 레이어에 batch normalization을 적용하여 input을 standardize 시킵니다.
레이어 순서는 다음과 같습니다.
Linear -> BatchNorm -> ReLU -> Linear -> ReLU
비교를 위해 GCN과 GIN 두가지 아키텍처를 구현했습니다.
GIN 코드를 보시면, 각 GINConv 레이어의 잠재 벡터를 h1, h2, h3로 저장하고 각각 global add pooling을 적용합니다.
이후 세 가지 벡터를 concat하여 h로 표현합니다. 이러한 h를 Linear층에 입력하여 그래프 분류 작업을 수행합니다.
import torch
torch.manual_seed(0)
import torch.nn.functional as F
from torch.nn import Linear, Sequential, BatchNorm1d, ReLU, Dropout
from torch_geometric.nn import GCNConv, GINConv
from torch_geometric.nn import global_mean_pool, global_add_pool
class GCN(torch.nn.Module):
"""GCN"""
def __init__(self, dim_h):
super(GCN, self).__init__()
self.conv1 = GCNConv(dataset.num_node_features, dim_h)
self.conv2 = GCNConv(dim_h, dim_h)
self.conv3 = GCNConv(dim_h, dim_h)
self.lin = Linear(dim_h, dataset.num_classes)
def forward(self, x, edge_index, batch):
# Node embeddings
h = self.conv1(x, edge_index)
h = h.relu()
h = self.conv2(h, edge_index)
h = h.relu()
h = self.conv3(h, edge_index)
# Graph-level readout
hG = global_mean_pool(h, batch)
# Classifier
h = F.dropout(hG, p=0.5, training=self.training)
h = self.lin(h)
return F.log_softmax(h, dim=1)
class GIN(torch.nn.Module):
"""GIN"""
def __init__(self, dim_h):
super(GIN, self).__init__()
self.conv1 = GINConv(
Sequential(Linear(dataset.num_node_features, dim_h),
BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU()))
self.conv2 = GINConv(
Sequential(Linear(dim_h, dim_h), BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU()))
self.conv3 = GINConv(
Sequential(Linear(dim_h, dim_h), BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU()))
self.lin1 = Linear(dim_h*3, dim_h*3)
self.lin2 = Linear(dim_h*3, dataset.num_classes)
def forward(self, x, edge_index, batch):
# Node embeddings
h1 = self.conv1(x, edge_index)
h2 = self.conv2(h1, edge_index)
h3 = self.conv3(h2, edge_index)
# Graph-level readout
h1 = global_add_pool(h1, batch)
h2 = global_add_pool(h2, batch)
h3 = global_add_pool(h3, batch)
# Concatenate graph embeddings
h = torch.cat((h1, h2, h3), dim=1)
# Classifier
h = self.lin1(h)
h = h.relu()
h = F.dropout(h, p=0.5, training=self.training)
h = self.lin2(h)
return F.log_softmax(h, dim=1)def train(model, loader):
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
epochs = 100
model.train()
for epoch in range(epochs+1):
total_loss = 0
acc = 0
val_loss = 0
val_acc = 0
# Train on batches
for data in loader:
optimizer.zero_grad()
out = model(data.x, data.edge_index, data.batch)
loss = criterion(out, data.y)
total_loss += loss / len(loader)
acc += accuracy(out.argmax(dim=1), data.y) / len(loader)
loss.backward()
optimizer.step()
# Validation
val_loss, val_acc = test(model, val_loader)
# Print metrics every 20 epochs
if(epoch % 20 == 0):
print(f'Epoch {epoch:>3} | Train Loss: {total_loss:.2f} | Train Acc: {acc*100:>5.2f}% | Val Loss: {val_loss:.2f} | Val Acc: {val_acc*100:.2f}%')
return model
@torch.no_grad()
def test(model, loader):
criterion = torch.nn.CrossEntropyLoss()
model.eval()
loss = 0
acc = 0
for data in loader:
out = model(data.x, data.edge_index, data.batch)
loss += criterion(out, data.y) / len(loader)
acc += accuracy(out.argmax(dim=1), data.y) / len(loader)
return loss, acc
def accuracy(pred_y, y):
"""Calculate accuracy."""
return ((pred_y == y).sum() / len(y)).item()
gcn = GCN(dim_h=32)
gcn = train(gcn, train_loader)
test_loss, test_acc = test(gcn, test_loader)
print(f'Test Loss: {test_loss:.2f} | Test Acc: {test_acc*100:.2f}%')
print()GCN은 73.18%의 정확도를 보였습니다.
### result ###
Epoch 0 | Train Loss: 0.67 | Train Acc: 58.24% | Val Loss: 0.69 | Val Acc: 58.84%
Epoch 20 | Train Loss: 0.61 | Train Acc: 71.64% | Val Loss: 0.59 | Val Acc: 71.33%
Epoch 40 | Train Loss: 0.59 | Train Acc: 71.50% | Val Loss: 0.59 | Val Acc: 69.76%
Epoch 60 | Train Loss: 0.60 | Train Acc: 70.75% | Val Loss: 0.58 | Val Acc: 68.92%
Epoch 80 | Train Loss: 0.59 | Train Acc: 72.37% | Val Loss: 0.62 | Val Acc: 69.70%
Epoch 100 | Train Loss: 0.59 | Train Acc: 69.55% | Val Loss: 0.58 | Val Acc: 71.11%
Test Loss: 0.61 | Test Acc: 73.18%GCN과 비교하여 GIN이 그래프 분류에 더욱 향상된 성능을 보여줍니다.
gin = GIN(dim_h=32)
gin = train(gin, train_loader)
test_loss, test_acc = test(gin, test_loader)
print(f'Test Loss: {test_loss:.2f} | Test Acc: {test_acc*100:.2f}%')
### result ###
Epoch 0 | Train Loss: 1.36 | Train Acc: 53.68% | Val Loss: 0.76 | Val Acc: 53.37%
Epoch 20 | Train Loss: 0.49 | Train Acc: 76.56% | Val Loss: 0.54 | Val Acc: 75.02%
Epoch 40 | Train Loss: 0.48 | Train Acc: 76.38% | Val Loss: 0.53 | Val Acc: 76.30%
Epoch 60 | Train Loss: 0.47 | Train Acc: 77.56% | Val Loss: 0.52 | Val Acc: 76.58%
Epoch 80 | Train Loss: 0.48 | Train Acc: 77.43% | Val Loss: 0.54 | Val Acc: 76.08%
Epoch 100 | Train Loss: 0.48 | Train Acc: 77.43% | Val Loss: 0.52 | Val Acc: 74.45%
Test Loss: 0.56 | Test Acc: 75.00%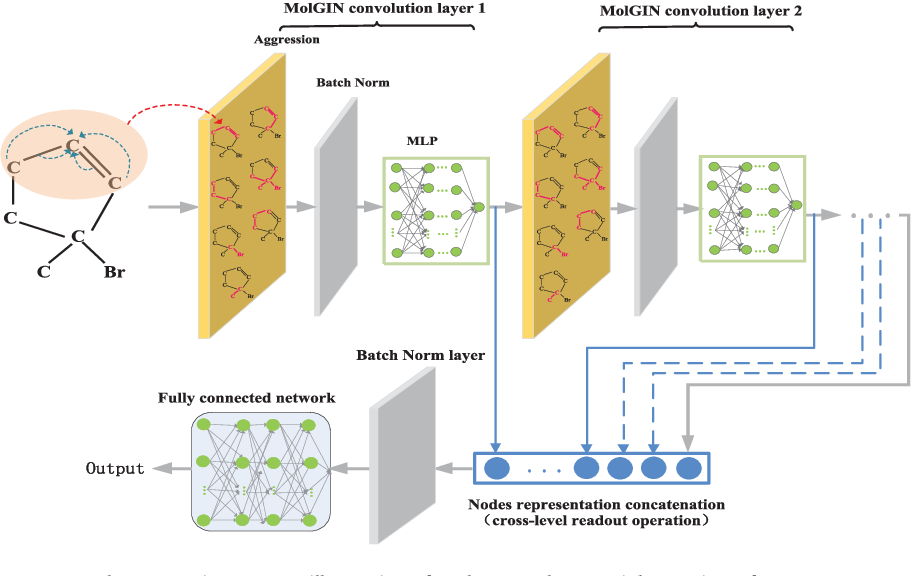
본 포스팅을 통해 PROTEINS 데이터셋에서 GIN 모델을 구현했습니다. GIN은 WL 테스트와 동등한 표현력을 갖는 강력한 GNN 아키텍처라는 것을 알아보았습니다. GIN은 그래프 분류 작업을 위해 글로벌 풀링 기법을 통해 노드 임베딩을 그래프 임베딩으로 변환합니다. 위 섹션에서 그래프 분류 작업에서 GIN과 GCN 모델을 비교하고, PROTEINS 데이터셋에서의 결과를 분석했습니다.
Reference
Hands-On Graph Neural Networks Using Python, published by Packt.
'Graph > Graph with Code' 카테고리의 다른 글
| 10. GNN을 활용한 그래프 생성 코드 구현하기 (0) | 2023.07.10 |
|---|---|
| 9. 그래프를 활용한 링크 예측(Link Prediction): 기초 방법론부터 GAE까지 (0) | 2023.07.07 |
| 7. GraphSAGE 이해 및 코드 구현 (7) | 2023.06.30 |
| 6. Graph Attention Networks (GATs) 기초 및 코드 구현 (0) | 2023.06.29 |
| 5. GCN 기초 및 코드 구현 (0) | 2023.06.28 |

