close
프로필 배경
프로필 로고

RecCode

Graph/Graph with Code · 2023. 6. 25. fullscreen 넓게보기

2. 그래프 기본 개념

 

 

Contents
1. 그래프 구조
1.1 그래프 종류
1.2 그래프 표현

2. 그래프 탐색 알고리즘
2.1 Breadth-first search
2.2 Depth-first search

3. 그래프 측정

 

본 포스팅에서는 이후 GNN을 다루기 위해 필요한 그래프에 대한 기본 개념들을 소개하겠습니다. 여러 그래프 구조와 그래프 알고리즘을 살펴볼 예정입니다. 본 포스팅에서는 networkx를 사용하여 코드를 통해 그래프를 그려볼 예정입니다.

 

필요한 라이브러리

  • networkx==2.8.8
  • matplotlib==3.6.3

1. 그래프 구조

1.1 그래프 종류

 

  그래프에서 특정 엔티티를 나타내는 노드(node)는 vertice라고도 표현한다. 따라서 노드를 V, 엣지를 E로 표현하면, 전체 그래프 G는 아래 수식과 같이 표현한다.

$$ G = (V,E) $$

 

그래프는 엣지의 방향성 여부에 따라, directed graph와 undirected graph로 구분된다.

  • Directed graph: 두 노드가 화살표를 가지고 연결되었으며, 한 노드에서 다른 노드로 가는 경로가 방향성을 가진다. (A->B)
  • Undirected graph: 방향을 갖지 않는 엣지들로 구성된 그래프이다. (A-B)

 

import networkx as nx
import matplotlib.pyplot as plt

# Directed graph

DG = nx.DiGraph()
DG.add_edges_from([('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'F'), ('C', 'G')])

plt.axis('off')
nx.draw_networkx(DG,
                 pos=nx.spring_layout(G, seed=0),
                 node_size=600,
                 cmap='coolwarm',
                 font_size=14,
                 font_color='white'
                 )

# Undirected graph

G = nx.Graph()
G.add_edges_from([('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'F'), ('C', 'G')])

plt.axis('off')
nx.draw_networkx(G,
                 pos=nx.spring_layout(G, seed=0),
                 node_size=600,
                 cmap='coolwarm',
                 font_size=14,
                 font_color='white'
                 )

 

방향성 외에 또다른 그래프 성질로는 weighted or unweighted가 있다. 엣지 가중치는 거리, 여행 시간, 비용과 같은 다양한 요소를 포함한다. 이러한 엣지 가중치는 보통, 노드가 binary일 때 사용한다. 또한 엣지는 단순히 둘 간의 관계 여부를 표시한다.

 

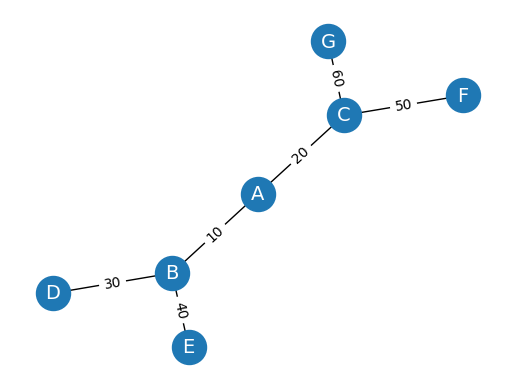
  • Weighted graph:각각의 엣지에 가중치 또는 비용을 할당한 그래프를 의미한다.
# Weighted graph

WG = nx.Graph()
WG.add_edges_from([('A', 'B', {"weight": 10}), ('A', 'C', {"weight": 20}), ('B', 'D', {"weight": 30}), ('B', 'E', {"weight": 40}), ('C', 'F', {"weight": 50}), ('C', 'G', {"weight": 60})])
labels = nx.get_edge_attributes(WG, "weight")

plt.axis('off')
nx.draw_networkx(WG,
                 pos=nx.spring_layout(G, seed=0),
                 node_size=600,
                 cmap='coolwarm',
                 font_size=14,
                 font_color='white'
                 )

 

  • Connected graph: 그래프끼리 노드가 하나로도 연결되어 있으면 connected graph라고 표현할 수 있다.
  • Rooted tree: 하나의 노드가 루트로 지정되고, 나머지 노드들은 상하 관계로 연결된 트리 구조이다.
  • Directed acyclic graph: 각각의 엣지에 방향을 가지고 있고, 순환 경로가 없는 그래프를 의미한다. 즉, 엣지들이 일방향으로만 향하며, 시작점에서 도착점으로 가는 어떤 경로도 순환하지 않는다. 이러한 특성으로 인해 DAG는 시간적인 순서나 의존 관계를 나타내는 데 많이 사용된다.
  • Bipartite graph (이분 그래프): 노드들을 두 개의 그룹으로 나누어 각 그룹 내의 노드들끼리는 서로 연결되지 않고, 다른 그룹에 속한 노드들과만 연결된 그래프를 의미한다. 특히 추천 시스템에서 유저와 아이템 간의 관계를 나타낼 때 유용한 개념이다.
  • Complete graph: 그래프 내의 모든 노드들이 서로 연결된 그래프를 의미한다. 즉, 모든 노드 쌍 간에 엣지가 존재하며, 그래프의 모든 가능한 엣지가 채워진 상태이다.

유저와 책 사이의 관계를 나타내는 이분 그래프

 


 1.2 그래프 표현

그래프 구조를 수학적으로 나타내기 위해, 그래프에 대한 여러가지 표현이 존재한다.

 

Adjacency matrix

먼저 인접 행렬을 아래와 같이 각 노드에 대해 연결 여부를 0,1 값을 가진 행렬로 나태난다. 인접 행렬은 2차원 배열로 시각화하기 쉬운 직관적인 표현 방법이다. 인접 행렬을 사용하는 주요 장점 중 하나는 두 노드가 연결되어 있는지 확인하는 것이 가능하다는 것이다. 이로써 그래프 내의 엣지 존재 여부를 효율적으로 확인할 수 있다. 또한, 인접 행렬은 최단 경로를 계산하는 등의 특정 그래프 알고리즘에서 유용한 행렬 연산을 수행하는 데 사용된다.

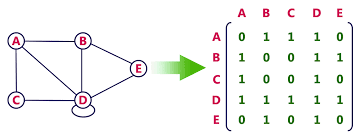
하지만, 노드의 추가 또는 제거에 따른 비용이 크게 발생할 수 있다. 이는 행렬의 크기를 조정하거나 이동해야 하기 때문이다. 인접 행렬의 주요 단점 중 하나로 공간 복잡도가 있다. 그래프 내의 노드 수가 증가함에 따라 인접 행렬을 저장하기 위해 필요한 공간이 기하급수적으로 증가한다.

 

Edge list

또한 노드간의 연결 관계만을 리스트 형태로 만드는 edge list 방법이 있다. 아래와 같이 엣지들의 리스트를 표현한다.

edge_list = [(0, 1), (0, 2), (1, 3), (1, 4), (2, 5), (2, 6)]

이러한 엣지 리스트는 연결된 관계만을 표현하기 때문에 인접 행렬에 비해 더욱 간결하다.

 

Adjacency list

또 다른 표현 방법은 인접 리스트이다. 이는 각 쌍이 그래프의 노드와 해당 노드의 인접 노드를 나타내는 딕셔너리로 구성된다. 아래와 같이 각 노드에 대한 연결된 노드들만 표현한다.

 

adj_list

{ 0: [1, 2],

1: [0, 3, 4],

2: [0, 5, 6],

3: [1],

4: [1],

5: [2],

6: [2] }

 

2. 그래프 탐색 알고리즘

그래프 알고리즘은 그래프 구조로 된 데이터를 이해하고, 학습하기 위해 중요하게 사용된다. 기본적인 그래프 탐색 알고리즘으로 BFS와 DFS를 살펴보겠다.

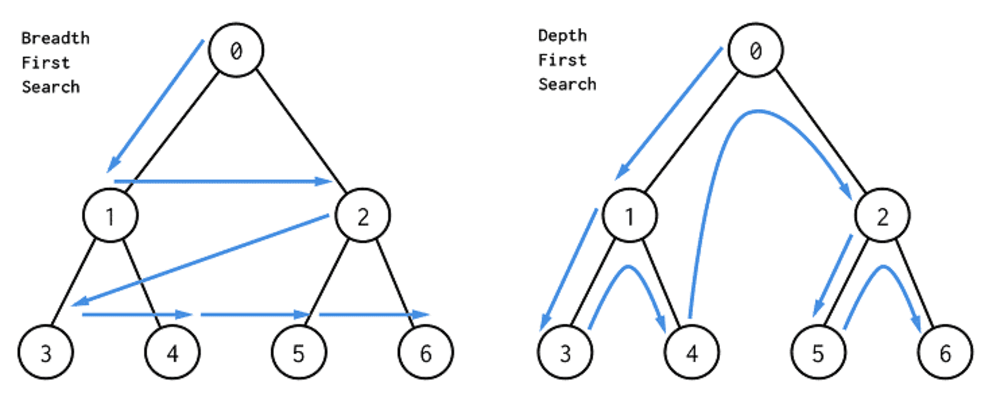
https://velog.velcdn.com/images/hbtopkr/post/69f77b7f-c12f-4e05-b9a9-dfb6ede63eb2/image.png

2.1 Breadth-first search

BFS는 시작 노드에서부터 인접한 모든 노드를 탐색한 다음, 그 다음 단계로 진행하여 더 멀리 있는 노드를 탐색하는 알고리즘이다. BFS는 큐(Queue) 자료구조를 사용하여 구현한다. 한 번 방문한 노드는 큐에 저장되고, 인접한 노드를 탐색한 뒤에는 큐의 선입선출(FIFO) 원칙에 따라 순차적으로 탐색한다. BFS는 최단 경로를 찾거나 노드 간의 거리를 계산하는 데 유용한 알고리즘이다.

# 1. 그래프를 생성한다.
G = nx.Graph()
G.add_edges_from([('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'F'), ('C', 'G')])

# 2. bfs를 계산하는 함수를 정의한다.
# 정의된 함수는 graph와 node를 입력으로 받는다.
def bfs(graph, node):

# 3. 두 개의 리스트를 생성한 후 시작 노드를 저장한다.
# visited: search 동안 탐색한 노드들을 저장함.
# queue: 탐색이 필요한 노드들을 저장함 (인접 노드).
    visited, queue = [node], [node]

# queue 리스트가 비워질 때까지 루프를 지속한다.
    while queue:
        node = queue.pop(0)
        for neighbor in graph[node]:
            if neighbor not in visited:
                visited.append(neighbor)
                queue.append(neighbor)

    return visited

bfs(G, 'A')
### result ###

['A', 'B', 'C', 'D', 'E', 'F', 'G']


2.2 Depth-first search

DFS는 깊이를 우선으로 탐색하는 알고리즘으로, 한 경로를 최대한 깊게 탐색한 후, 다음 경로로 넘어간다. DFS는 스택(Stack) 자료구조를 사용하여 구현된다. 즉, 한 번 방문한 노드는 스택에 저장되고, 해당 노드의 인접한 노드를 탐색하기 전까지 계속해서 현재 경로를 따라 진행한다. DFS는 그래프의 구조를 파악하는 데 유용하며, 사이클 여부를 확인하거나 그래프의 깊이 우선적인 속성을 탐색하는 데 사용된다.

 

DFS를 구현하는 코드는 재귀적인 알고리즘을 사용한다.

# 1. 탐색 노드를 저장하기 위한 빈리스트 생성
visited = []

# 2. dfs 함수는 탐색 리스트와, 그래프, 노드를 입력 받음.
def dfs(visited, graph, node):

# 3. 현재 노드가 visited에 없다면, 노드를 visited에 추가함.
    if node not in visited:
        visited.append(node)
# 4. 현재 노드의 이웃들을 순회한다.
    # 이때, 각 이웃마다 dfs를 다시 호출하여 탐색한다.
        for neighbor in graph[node]:
            visited = dfs(visited, graph, neighbor)
# 5. dfs() 함수는 각 노드의 모든 이웃을 방문한다.
    # 최종적으로 visited 리스트가 반환된다.
    return visited

dfs(visited, G, 'A')
### result ###

['A', 'B', 'D', 'E', 'C', 'F', 'G']

 

3. 그래프 측정

그래프 측정(Graph measures)은 그래프의 노드나 엣지에 대한 중요성이나 중심성을 측정하는 방법을 의미한다. 이러한 측정은 그래프의 구조와 연결성을 분석하고 이해하는 필요하다. 주요한 그래프 측정 방법 세가지는 다음과 같다.

 

  1. Degree centrality (연결 중심성): Degree centrality는 노드의 연결 정도를 측정하는 방법이다. 특정 노드의 연결된 엣지 수를 해당 노드의 중심성으로 간주한다. Degree centrality가 높을수록 해당 노드는 그래프 내에서 중요한 역할한다는 것을 의미한다. 네트워크에서의 사회적인 영향력이나 정보 전달의 중심 등을 측정하는 데 사용된다.
  2. Closeness centrality (근접 중심성): Closeness centrality는 특정 노드와 다른 노드 간의 근접성을 측정하는 방법이다. 특정 노드에서 다른 모든 노드까지의 최단 경로의 평균 거리를 해당 노드의 중심성으로 간주한다. Closeness centrality가 높을수록 해당 노드는 다른 노드와의 근접성이 높으며, 정보의 전달이 빠르고 효율적으로 이루어질 가능상이 높다.
  3. Betweenness centrality (매개 중심성): Betweenness centrality는 그래프 내에서 특정 노드가 다른 노드들 간의 최단 경로 상에서 얼마나 중간에 위치하는지를 측정하는 방법이다. 특정 노드가 다른 노드들 간의 통로 역할을 하는 정도를 측정한다. Betweenness centrality가 높은 노드는 병목 현상의 중간 지점으로 이해될 수 있으며, 다른 노드들 간의 통신, 정보 전달, 영향력 전파 등에서 중개자 역할을 수행한다.

 

G = nx.Graph()
G.add_edges_from([('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'F'), ('C', 'G')])

print(f"Degree centrality      = {nx.degree_centrality(G)}")
print(f"Closeness centrality   = {nx.closeness_centrality(G)}")
print(f"Betweenness centrality = {nx.betweenness_centrality(G)}")
### result ###

Degree centrality      = {'A': 0.3333333333333333, 'B': 0.5, 'C': 0.5, 'D': 0.16666666666666666, 'E': 0.16666666666666666, 'F': 0.16666666666666666, 'G': 0.16666666666666666}
Closeness centrality   = {'A': 0.6, 'B': 0.5454545454545454, 'C': 0.5454545454545454, 'D': 0.375, 'E': 0.375, 'F': 0.375, 'G': 0.375}
Betweenness centrality = {'A': 0.6, 'B': 0.6, 'C': 0.6, 'D': 0.0, 'E': 0.0, 'F': 0.0, 'G': 0.0}

 

Reference 

Hands-On Graph Neural Networks Using Python, published by Packt.

반응형

'Graph > Graph with Code' 카테고리의 다른 글

6. Graph Attention Networks (GATs) 기초 및 코드 구현  (0) 2023.06.29
5. GCN 기초 및 코드 구현  (0) 2023.06.28
4. GNN 기초 (직접 코드로 구현하기)  (0) 2023.06.27
3. 노드 임베딩 (Node2Vec으로 간단한 추천시스템 구현)  (0) 2023.06.26
1. 그래프 이해하기  (0) 2023.06.24
Graph/Graph with Code 관련 글
더 보기

티스토리툴바